DETERMINANTES
Definición de determinante
A cada matriz cuadrada A se le asigna un escalar particular denominado determinante de A , denotado por |A| o por det (A).
Determinante de orden uno
|a 11| = a 11
Determinante de orden dos

= a
11 a
22 − a
12 a
21
Determinante de orden tres

=
a11 a22 a33 + a12 a23 a31 + a13 a21 a32 −
− a 13 a22 a31 − a12 a21 a 33 − a11 a23 a32.
Los términos con signo + están formados por los elementos de la diagonal principal y los de las diagonales paralelas con su correspondiente vértice opuesto.
Los términos con signo − están formados por los elementos de la diagonal secundaria y los de las diagonales paralelas con su correspondiente vértice opuesto.
IMAGEN DE LOS DETERMINANTES






 TIENE UNA SOLUCION
TIENE UNA SOLUCION TIENE INFINITAS SOLUCIONES
TIENE INFINITAS SOLUCIONES NO TIENE SOLUCION LAS RECTAS SON PARALELAS
NO TIENE SOLUCION LAS RECTAS SON PARALELAS










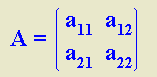


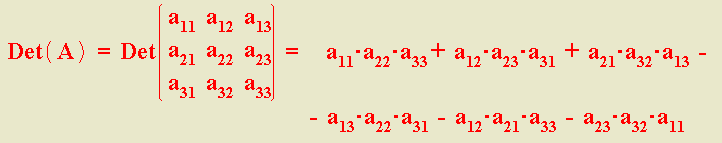


 = a 11 a 22 − a 12 a 21
= a 11 a 22 − a 12 a 21 =
=














