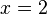SISTEMA DE ECUACIONES LINEALES CON DOS VARIABLES POR REDUCCION
El método de reducción consiste en multiplicar cada una de las ecuaciones por los valores necesarios, de forma que los coeficientes de una de las incógnitas sean los mismos cambiados de signo. Conseguido esto, se suman las dos ecuaciones y la incógnita que tiene los coeficientes opuestos se elimina, dando lugar a una ecuación con una incógnita, que se resuelve haciendo las operaciones necesarias. Conocida una de las incógnitas se sustituye su valor en una de las ecuaciones originales y calculamos la segunda.
tenemos como ejemplo el sistema:

En este caso la x, ya tiene el mismo coeficiente en las dos ecuaciones cambiado de signo y no es necesario hacer ninguna operación para lograrlo; podemos sumar las dos ecuaciones directamente:

como resultado de la suma tenemos una sola ecuación con una incógnita:

despejando la y, tenemos:

que haciendo la operación da:

Para calcular el valor de x, sustituimos el valor de y en una de las ecuaciones, por ejemplo la primera:

despejando x, tenemos:

que realizando la operación da como resultado:
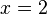
el resultado del sistema es el valor de x e y que satisface las dos ecuaciones simultáneamente, que como ya sabíamos es:
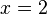

En este caso era muy fácil dado que la x ya tenía el mismo coeficiente cambiado de signo en una y otra ecuación. Podemos resolver el mismo sistema, pero esta vez eliminando la y:

vemos el coeficiente de la y de la primera ecuación es 1 y el de la segunda, 2; si multiplicamos la primera ecuación por 2, y la segunda la cambiamos de signo, tendremos:

con lo que tenemos que la y tiene el mismo coeficiente en las dos ecuaciones cambiado de signo. Sumando las dos ecuaciones:

así tenemos una ecuación con una incógnita:

despejando la x:

el valor de x que obtenemos es:
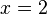
para calcular y sustituimos el valor obtenido de x en una de las ecuaciones, la primera de ellas por ejemplo:

que despejando la y tendremos:

con lo que tenemos:

Como puede verse en el ejemplo resuelto, el método de reducción consiste en operar el sistema de modo que una de las incógnitas tenga el mismo coeficiente en las dos ecuaciones pero cambiado de signo; al sumar las dos ecuaciones el sistema se reduce a una ecuación con una incógnita que despejamos. Con este valor sustituido en una de las ecuaciones iniciales calculamos la segunda incógnita. Es indistinto que se haga con la x o con la y, en los dos casos obtendremos el mismo resultado.