MULTIPLICACIÓN DE FRACCIONES ALGEBRAICAS
El producto de dos fracciones algebraicas es otra fracción algebraica donde el numerador es el producto de los numeradores y el denominador es el producto de los denominadores. | |
Primero hay que facto rizar totalmente a todos los polinomios que se puedan en ambas fracciones. Luego, se simplifican los polinomios que "aparezcan repetidos", siempre tachando "uno de arriba con uno de abajo", como en este caso el binomio (x + 3), que está en el denominador de la primera fracción y en el numerador de la segunda. Finalmente hay que multiplicar las fracciones que quedaron, del mismo modo que se multiplican las fracciones numéricas: numerador con numerador, y denominador con denominador.
Y si lo piden, aclarar que la simplificación vale solamente para x ≠ 3.
EJEMPLO 1:
1 EJEMPLO 2: 1 1 2.(x + 1) | |
EJEMPLO 3:
1 1 EJEMPLO 4: 1
IMAGENES DE LA MULTIPLICACION DE FRACCIONES ALGEBRAICAS
1 | |
Matemática Décimo
lunes, 30 de mayo de 2016
DEFINICION DE MULTIPLICACION DE FRACCIONES ALGEBRAICAS Y EJERCICIOS
SUMA Y RESTA DE FRACCIONES ALGEBRAICAS CON DISTINTO DENOMINADOR
SUMA Y RESTA DE FRACCIONES ALGEBRAICAS CON DISTINTO DENOMINADOR
REGLA.- Se sigue el mismo procedimiento de la suma y resta de fracciones numèricas con distinto denominador
Ejemplo






 IMAGENES DE SUMA Y RESTA DE FRACCIONES ALGEBRAICAS CON DISTINTO DENOMINADOR
IMAGENES DE SUMA Y RESTA DE FRACCIONES ALGEBRAICAS CON DISTINTO DENOMINADOR

Sumar y restar las fracciones algebraicas:






 IMAGENES DE SUMA Y RESTA DE FRACCIONES ALGEBRAICAS CON DISTINTO DENOMINADOR
IMAGENES DE SUMA Y RESTA DE FRACCIONES ALGEBRAICAS CON DISTINTO DENOMINADORmiércoles, 27 de abril de 2016
SUMA DE FRACCIONES ALGEBRAICAS CON EL MISMO DENOMINADOR
SUMA DE FRACCIONES ALGEBRAICAS CON EL MISMO DENOMINADOR
La suma de fracciones algebraicas con el mismo denominador es otra fracción algebraica con el mismo denominador y cuyo numerador es la suma de los numeradores.
Ejemplo
Sumar las fracciones algebraicas:




IMAGEN DE LA SUMA DE FRACCIONES ALGEBRAICAS CON EL MISMO DENOMINADOR
lunes, 25 de abril de 2016
SIMPLIFICACION DE FRACCIONES ALGEBRAICAS
SIMPLIFICACION DE EXPRESIONES ALGEBRAICAS RACIONALES / EJERCICIOS RESUELTOS | |
EJEMPLO 1:
Hay que factorizar todo lo que se pueda, tanto en el numerador como en el denominador. En el numerador apliqué el 5to Caso (Diferencia de Cuadrados); y en el denominador, el 1er Caso (Factor Común). Luego, se simplifican los polinomios que "aparezcan repetidos", siempre tachando "uno de arriba con uno de abajo", como en este caso el binomio (x - 2). Condición para simplificar: x desigual a 2. EXPLICACIÓN DEL EJEMPLO 1 EJEMPLO 2: ("Cuando se cancela todo el denominador") En este ejemplo se simplificó el único polinomio que había en el denominador. El resultado es lo que queda sin tachar en el numerador de la fracción. Condición para simplificar: x desigual a -3. EXPLICACIÓN DEL EJEMPLO 2 EJEMPLO 3: ("Cuando se cancela todo el numerador") En este ejemplo se simplificó el único polinomio que había en el numerador. Entonces la fracción queda con un "1" como numerador. Condición para simplificar: x desigual a -4. EXPLICACIÓN DEL EJEMPLO 3 EJEMPLO 4: (Se simplifica un polinomio que está elevado al cuadrado) Hay un polinomio al cuadrado que se puede simplicar con otro. Tacho el "2" del cuadrado y tacho el otro polinomio. Condición para simplificar: x desigual a 3. EXPLICACIÓN DEL EJEMPLO 4 EJEMPLO 5: ("Cuando se simplifica la x") Después de factorizar, queda la "x" (o cualquier letra del polinomio) multiplicando tanto en el numerador como en el denominador, entonces se puede simplicar. Condición para simplificar: x desigual a 0. EXPLICACIÓN DEL EJEMPLO 5 | |
EJEMPLO 6: ("Cuando quedan números para simplicar") Después de factorizar, quedan números multiplicando tanto en el numerador como en el denominador. El "6" y el "8" se pueden simplificar dividiendo por 2 (como en las fracciones numéricas). Condición para simplificar: ninguna. EXPLICACIÓN DEL EJEMPLO 6 EJEMPLO 7: ("Cuando los números que quedan son fracciones") 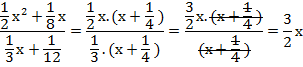 Después de factorizar, quedan fracciones multiplicando en el numerador y en el denominador. Se puede dividir la fracción de "arriba" con la de "abajo" para que quede una sola fracción en el resultado. Aquí dividí 1/2 : 1/3 = 3/2. Condición para simplificar: ninguna. EXPLICACIÓN DEL EJEMPLO 7 MÁS EJEMPLOS: EJEMPLO 8: EXPLICACIÓN DEL EJEMPLO 8 EJEMPLO 9: EXPLICACIÓN DEL EJEMPLO 9 EJEMPLO 10: EXPLICACIÓN DEL EJEMPLO 10 EJEMPLO 11:
IMAGEN DE LA SIMPLIFICACION DE FRACCIONES
| |
Suscribirse a:
Entradas (Atom)